Beziér curves and JavaScript
You’ve no doubt already heard of Beziér curves and seen them being used in graphics packages and computer games. You may have even thought of using them to perform animations and transitions in DHTML, but maybe you were daunted by the complex mathematics involved.
While the underlying principles are reasonably advanced, it is not necessary for you to understand the Beziér Functions in order to use them.
Beziér functions can be used to generate a wide range of shapes, including 2D & 3D lines and 3D patches for modeling. This tutorial shows you how to use a cubic Beziér curve in 2-dimensions and uses the Bernstein Basis Function to calculate the points on the curve.
The Maths
The Bernstein Basis Function is as follows:
1 = t + (1 - t)
Obvious right? Try it out, substitute any value for t and you will find this equation holds true.
Now, we use this function as a parametric method for generating the complex
curves. For a quadratic (2nd order) Beziér curve we square both sides:
12 = (t + (1 - t))2
» 1 = t2 + 2t(1 - t) + (1 - t)2
And for a cubic (3rd order) curve we cube both sides:
13 = (t + (1 - t))3
» 1 = (t + (1 - t)) . (t2 + 2t(1 - t) + (1 - t)2)
» 1 = t3 + 3t2(1 - t) + 3t(1 - t)2 + (1 - t)3
 While it
is possible to simplify this equation more, for the purpose of this
we want it in terms of t and (1 - t). You should also note the way we
order the equation.
While it
is possible to simplify this equation more, for the purpose of this
we want it in terms of t and (1 - t). You should also note the way we
order the equation.
The cubic equation can be split up to give us 4 Beziér functions:
B1(t) = t3
B2(t) = 3t2(1 - t)
B3(t) = 3t(1 - t)2
B4(t) = (1 - t)3
In a quadratic (2nd order) curve there would only be 3 functions and in a quartic (4th order) there would be 5.
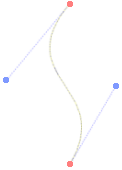
Now, a cubic Beziér curve is defined by 4 control points. The first being the
start point, the next 2 define the shape of the curve and the final point is the
end point.
To find a particular point on the curve we use the following equation:
p = C1.B1(d) + C2.B2(d) + C3.B3(d) + C4.B4(d)
where:
Ci are the control points
Bi are the Beziér functions
d is a percentage of the distance along the curve
(between 0 and 1)
p is the point in 2D space
Beziér Curves in JavaScript
To use Beziér Curves in JavaScript, we’ll begin by defining a custom type to represent the position of a point in 2D space:
coord = function (x,y) {
if(!x) var x=0;
if(!y) var y=0;
return {x: x, y: y};
}
In order to make it easier to program, we then need to define the Beziér Base Functions (see above):
function B1(t) { return t*t*t }
function B2(t) { return 3*t*t*(1-t) }
function B3(t) { return 3*t*(1-t)*(1-t) }
function B4(t) { return (1-t)*(1-t)*(1-t) }
We can then define the control points of the Beziér curve as a coord datatype:
C1 = coord(50,100); C2 = coord(-50,200); C3 = coord(150,400); C4 = coord(500,300);
Now using the equation described above we can find a point half way along the Beziér curve using the following code:
var pos = new coord(); pos.x = C1.x * B1(0.5) + C2.x * B2(0.5) + C3.x * B3(0.5) + C4.x * B4(0.5); pos.y = C1.y * B1(0.5) + C2.y * B2(0.5) + C3.y * B3(0.5) + C4.y * B4(0.5);
Putting this together we get the following function:
//====================================\\
// 13thParallel.org Beziér Curve Code \\
// by Dan Pupius (www.pupius.net) \\
//====================================\\
coord = function (x,y) {
if(!x) var x=0;
if(!y) var y=0;
return {x: x, y: y};
}
function B1(t) { return t*t*t }
function B2(t) { return 3*t*t*(1-t) }
function B3(t) { return 3*t*(1-t)*(1-t) }
function B4(t) { return (1-t)*(1-t)*(1-t) }
function getBezier(percent,C1,C2,C3,C4) {
var pos = new coord();
pos.x = C1.x*B1(percent) + C2.x*B2(percent) + C3.x*B3(percent) + C4.x*B4(percent);
pos.y = C1.y*B1(percent) + C2.y*B2(percent) + C3.y*B3(percent) + C4.y*B4(percent);
return pos;
}
Remember percent has to be between 0 and 1.
Examples
Example
1: Shows you how to use the
getBezier function to animate a nice
curve.
Example
2:
Uses one curve to define the point on another curve, gives a bouncing ball
effect (same method as used in the 13th API's timeSlide() function)
Example
3: Allows you to play with a
Beziér curve.
Example 4: a bouncing 3d cube courtesy of the guys over at Netzministerium, uses their 3dhtml
API.
References
This tutorial offers a very basic introduction to Beziér curves, just enough
to understand how the functions work. As well as helping me write this
tutorial, the links below provide some more detailed information on the maths
and use of Beziér curves.
Unraveling Beziér Splines by Justin Reynen (Gamedev.net)
Beziér Curves and
More on Beziér Curves by Ian E. Aitchison