Mathematics & DHTML
By Daniel Pupius, February 2002
Now it may seem that this site is going to be very Maths related but that's just a coincidence. I wrote this tutorial on Maths & DHTML because of several requests after the Beziér tutorial last month. This month we'll be looking at some basic mathematical principles and how they can be used to liven up your site and have some fun with DHTML.
Using timeouts
setTimeout() is a JavaScript function that is an integral part of animating
objects in DHTML, it allows us to run JavaScript code after a given delay. There are two methods that we can use (they will be
known as "method 1" and "method 2" throughout the tutorial).
Method 1 performs a step of the animation at each timeout, while easy this leads to problems with browsers that render the page slowly: CPU times and RAM can vary drastically, and the operating system and browser effect the time it takes to render a page.
To workaround this problem, the method 2 defines a specific amount of time for the animation to last. We can then calculate where in the animation the object should be each time we call a timeout - this means that on fast machines the animation will be nice and smooth, while it will appear jerky on slow machines it will still take the defined amount of time.
Example 1:
a very basic script that demonstrates animation between 2 points, specifying
explicitly how many pixels to move each iteration.
Example 2: performs a movement that lasts for a specified
amount of time.
Pythagoras
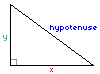 Pythagoras' theorem states:
Pythagoras' theorem states:
"The square of the hypotenuse of a right angled triangle is equal to the sum of the squares of
the other two sides."
i.e.
(hypotenuse)2 = x2 + y2
or
hypotenuse = √(x2 + y2)
Now, this is very useful when performing animations as if we know the coordinates of 2 points then we can calculate the distance between them.
So in JavaScript:
function distance(x1,y1,x2,y2) {
//find horizontal distance (x)
var x = x2 - x1;
//find vertical distance (y)
var y = y2 - y1;
//do calculation
var hyp = Math.sqrt(x*x + y*y);
return hyp;
}
Trigonometry
Trigonometry is a fundamental part of mathematics and like Pythagoras is based around right-angled triangles. Its applications are extensive and provides a base for more complex mathematics such calculus, linear algebra and statistics.
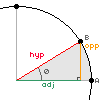 The
diagram on the right shows a right-angled triangle as part of a circle.
Theta (θ) is the angle traced out by a point moving from A to B around the
circle, we can then make a right-angled triangle with a hypotenuse (hyp), a
line opposite the angle (opp) and a line adjacent to the angle (adj) - the
right-angle is formed between the opposite and the adjacent. We can now
define any point on a circle using a right angled triangle.
The
diagram on the right shows a right-angled triangle as part of a circle.
Theta (θ) is the angle traced out by a point moving from A to B around the
circle, we can then make a right-angled triangle with a hypotenuse (hyp), a
line opposite the angle (opp) and a line adjacent to the angle (adj) - the
right-angle is formed between the opposite and the adjacent. We can now
define any point on a circle using a right angled triangle.
In order to calculate the various lines and angles on this diagram we use
three basic functions and their inverses:
tan θ = opp / adj
sin θ = opp / hyp
cos θ = adj / hyp
These are the "tangent of an angle", "sine of an angle"
and the "cosine of an angle" respectively.
Their inverses are as follows, such that f(f-1(x)) = x:
θ = tan-1(opp / adj) or θ = atan(opp / adj)
θ = sin-1(opp / hyp) or θ = asin(opp / hyp)
θ = cos-1(adj / hyp) or θ = acos(adj / hyp)
Now, we would use the first three functions to calculate the other sides of a right-angled triangle if we already know the values of the angle and one side. The inverses are used to find the angles in a triangle if we already know the values of two sides, in practice we only normally use atan and Pythagoras.
In JavaScript the following functions exist as part of the Math object and are particularly useful (there are a couple more that we rarely need to use):
Math.tan(angle); // Tangent of an angle Math.sin(angle); // Sine of an angle Math.cos(angle); // Cosine of an angle // Returns an angle between 2 sides // (between PI and -PI radians) Math.atan2(opp,adj);
Angles can be measured in terms of two different units, degrees and radians, with a circle being made up of 360-degrees (360°) or 2pi radians.
Generally it is easier to think in terms of degrees, however all the Math functions use radians. It is therefore a good idea to create a couple of functions that can flip between the two:
function degToRad(angle) {
return ((angle*Math.PI) / 180);
}
function radToDeg(angle) {
return ((angle*180) / Math.PI);
}
Example 3 : Using trigonometry animate an object in a circle (demo of key principles)
Motion under constant acceleration
The following equations are very useful in calculations with moving bodies:
v = u + at
s = ut + ½at2
v2 = u2 + 2as
s = ½t(u + v)
where:
v = velocity at end of movement
u = velocity at start of movement
a = acceleration
t = time
s = displacement (distance with sign as well as magnitude)
For simple acceleration we can
simply increase the speed by a set amount after each iteration:
v += a
x += v
Example 4 - demonstration of acceleration
Motion in 2D
So far, with exception of the circle, the examples have only shown movement in 1-dimension. We'll now have a look at using Pythagoras, Trigonometry and Acceleration to move an object between two arbitrary points on the page.
Method 1
The first thing we do is find
the angle between the start position and the end position:
θ = atan ( (y2-y1) / (x2-x1) )
where (x1,y1) is the object's current coordinates and (x2,y2) is the destination
coordinates.
We then use this result to find the horizontal and vertical components of the
velocity:
vx = v * cos(θ)
vy = v * sin(θ)
Now, at each iteration we increment the objects coordinates by (vx,vy).
This is all very well, however, how do we know when the animation has finished?
Well, we can use the distance function defined in the Pythagoras section and if the distance to the final destination is smaller than the velocity then the animation is over and we move the object to it's end position.
Method 2
If you remember, "method 2" defines a set amount of time for the animation to take place.
Again, we calculate the angle to the end point and we also calculate the
total distance to be covered:
θ = atan ( (y2-y1) / (x2-x1) )
Total Distance = √((x2 - x1)2 + (y2-y1)2)
If we keep track of how much time has passed since the start of the animation
then we can calculate what distance should have been covered so far:
Current Distance = Total Distance * Time Passed/Duration
We can then get:
x = x1 + [Current Distance]*cos(θ)
y = y1 + [Current Disance]*sin(θ)
Forces
This is just a bit of fun and shows two examples of forces applied to free moving objects (we'll call them particles). Since there is no destination for the particle we need to represent the velocity as a vector quantity (i.e. it has direction & magnitude). We could do this by having a X and Y component for velocity, but what is nicer, if a bit more complex, is to have an angle and a speed. We will make an object for the velocity:
var v = {speed: 0, angle: 0};
To move the particle you can simple increase the object's left & right style attributes at each timeout using:
x += v.speed * Math.cos(degToRad(v.angle)); y += v.speed * Math.sin(degToRad(v.angle));
Gravity
Gravity is a force that is only applied to the y component of velocity. The Earth's gravitational force is measured at 9.8m/s2. We could calculate how many pixels are in a meter (on average) and then work out the exact acceleration in pixels/s2, but we will just use a value that makes it look reasonable.
To update the velocity we need to convert it into x and y components, apply the acceleration and then convert it back to a vector, this may seem like a round about method but in the long term it is better to represent velocity as speed and direction.
var gravity = 1.5; var vx = v.speed * Math.cos(degToRad(v.angle)); var vy = v.speed * Math.sin(degToRad(v.angle)); vy += gravity; v.speed = Math.sqrt((vx*vx)+(vy*vy)); v.angle = Math.atan(vy,vx);
Bounding box
An example using the above code wouldn't be very interesting since the particles would quite soon fly off the screen. What we can do instead is reverse the particle when it hits a border:
var vx = v.speed * Math.cos(degToRad(v.angle)); var vy = v.speed * Math.sin(degToRad(v.angle)); if((x<0 && vx<0) || (x>maxX && vx>0)) vx *= -1; if((y<0 && vy<0) || (y>maxY && vx>0)) vy *= -1; v.speed = Math.sqrt((vx*vx)+(vy*vy)); v.angle = Math.atan2(vy,vx);
To make it even more realistic we can add a damping effect, where energy is lost when the particle hits a wall. This is easily done by multiplying by a number greater than minus-one but less than zero. e.g. -0.9
Friction
Friction is really simple. We simply reduce the speed by a certain quantity every iteration, e.g.
v.speed *= 0.9;
Example 9
- shows boxes bouncing around a container
Example 10 - shows boxes bouncing around a container effected by gravity
Example 11
- lots of little particles succumbing to friction
Example 12 - complex
example showing particles being "fired"
into a denser medium so that friction increases and gravity decreases
Conclusion
Well that's it. I hope at least a couple of people have learned something from this. I'd be very interested to hear your comments about this tutorial, especially any additions that might prove useful, also any mistakes I've made :)
Examples
Here’s a list of all the examples used in this tutorial:
Example 1 - a very basic script that demonstrates animation between 2 points, specifying
explicitly how many pixels to move each iteration
Example 2 - performs a movement that lasts for a specified amount of time
Example 3 - using trigonometry animate an object in a circle
Example 4 - demonstration of acceleration
Example 9 - shows boxes bouncing around a container
Example 10 - shows boxes bouncing around a container effected by gravity
Example 11 - lots of little particles succumbing to friction
Example 12 - complex example showing particles being “fired” into a denser medium so that friction increases and gravity decreases